Which is the best approximation for the measure of angle XYZ? 33.6 ° 39.8 ° 50.2 ° 56.4 °
Question

Answer:
The best measure of the angle ∠XYZ is given by: Option B: 39.8°What are the six trigonometric ratios?Trigonometric ratios for a right angled triangle are from the perspective of a particular non-right angle.In a right angled triangle, two such angles are there which are not right angled (not of 90 degrees).The slant side is called hypotenuse. From the considered angle, the side opposite to it is called perpendicular, and the remaining side will be called base.From that angle (suppose its measure is θ),[tex]\sin(\theta) = \dfrac{\text{Length of perpendicular}}{\text{Length of Hypotenuse}}\\\cos(\theta) = \dfrac{\text{Length of Base }}{\text{Length of Hypotenuse}}\\\\\tan(\theta) = \dfrac{\text{Length of perpendicular}}{\text{Length of base}}\\\\\cot(\theta) = \dfrac{\text{Length of base}}{\text{Length of perpendicular}}\\\\\sec(\theta) = \dfrac{\text{Length of Hypotenuse}}{\text{Length of base}}\\\\\csc(\theta) = \dfrac{\text{Length of Hypotenuse}}{\text{Length of perpendicular}}\\\\[/tex]The missing figure is attached below.From the given figure, if we see from the angle x which is ∠XYZ, the hypotenuse is YZ, perpendicular = XZ with length 10 inches, and base XY with length 12 inches.Since perpendicular and base are specified, we can directly use tangent ratio and then its inverse to find the measure of the ∠XYZ, as shown below:[tex]\tan(\angle XYZ) = \dfrac{|XZ|}{|XY|} = \dfrac{10}{12}\\\\\angle XYZ = \tan^{-1}\left(\dfrac{10}{12}\right) \approx 39.8^\circ[/tex]Thus, the best measure of the angle ∠XYZ is given by: Option B: 39.8°Learn more about inverse trigonometric functions here:
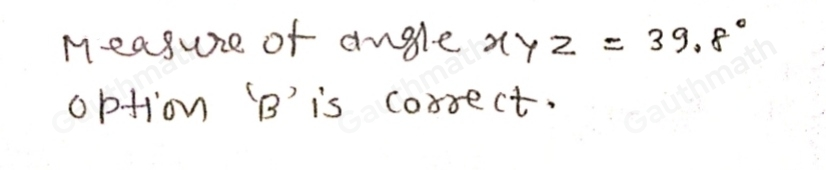

solved
algebra
11 months ago
8505