_ b. fx=x3+5x2-8x-11 Jawab:_
Question
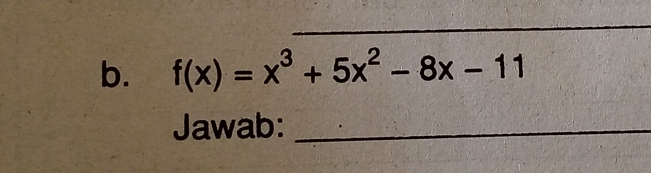
Answer:
Untuk mencari perpotongan x, atur y = 0: x^{3} + 5 x^{2} - 8 x - 11 = 0Pecahkan persamaannya: x = - 0.9327ataux = 1.9575ataux = - 6.0247Tentukan keberagamannya: Tidak adaUntuk menemukan perpotongan y, aturx = 0: f{(0 )} = 0^{3} + 5 \times 0^{2} - 8 \times 0 - 11Hitung daya: f{(0 )} = - 11Temukan domain fungsi tanpa batasan : x \in RTentukan jenis fungsinya : fungsi kubikTulis dalam bentuk standar: f{(x )} = x^{3} + 5 x^{2} - 8 x - 11Tulis dalam bentuk faktorisasi: Tidak adaTemukan f(-x): f{(- x )} = (- x)^{3} + 5 (- x)^{2} - 8 (- x) - 11Hapus tanda kurung: f{(- x )} = - x^{3} + 5 x^{2} + 8 x - 11Tentukan hubungan antara f(x) dan f(-x): f{(x )} \neq f{(- x )}Temukan -f(-x): - f{(- x )} = - (- x^{3} + 5 x^{2} + 8 x - 11)Hapus tanda kurung: - f{(- x )} = x^{3} - 5 x^{2} - 8 x + 11Tentukan hubungan antara f(x) dan -f(-x): f{(x )} \neq - f{(- x )}Tentukan paritasnya: Neither\ even\ nor\ oddTemukan x-intersep: Tidak adaTentukan interval kenaikan: [\dfrac{2}{3}, \infty) , (-\infty, -4]Tentukan interval penurunan: [-4, \dfrac{2}{3}]Temukan jumlah kemungkinan nol nyata in f{(x )} = x^{3} + 5 x^{2} - 8 x - 11:: 0Temukan jumlah kemungkinan titik balik: 2Tentukan derajatnya :: 3Temukan istilah utama: x^{3}Temukan koefisien terkemuka : 1Temukan istilah konstan : - 11Temukan ekstrema: (-4,37), (\dfrac{2}{3},- \dfrac{373}{27})Analisis perilaku akhir: sebagai x →\infty,f(x)→ \infty; sebagai x →-\infty,f(x)→ -\inftyBuat grafik fungsinya:
solved
algebra
11 months ago
8022