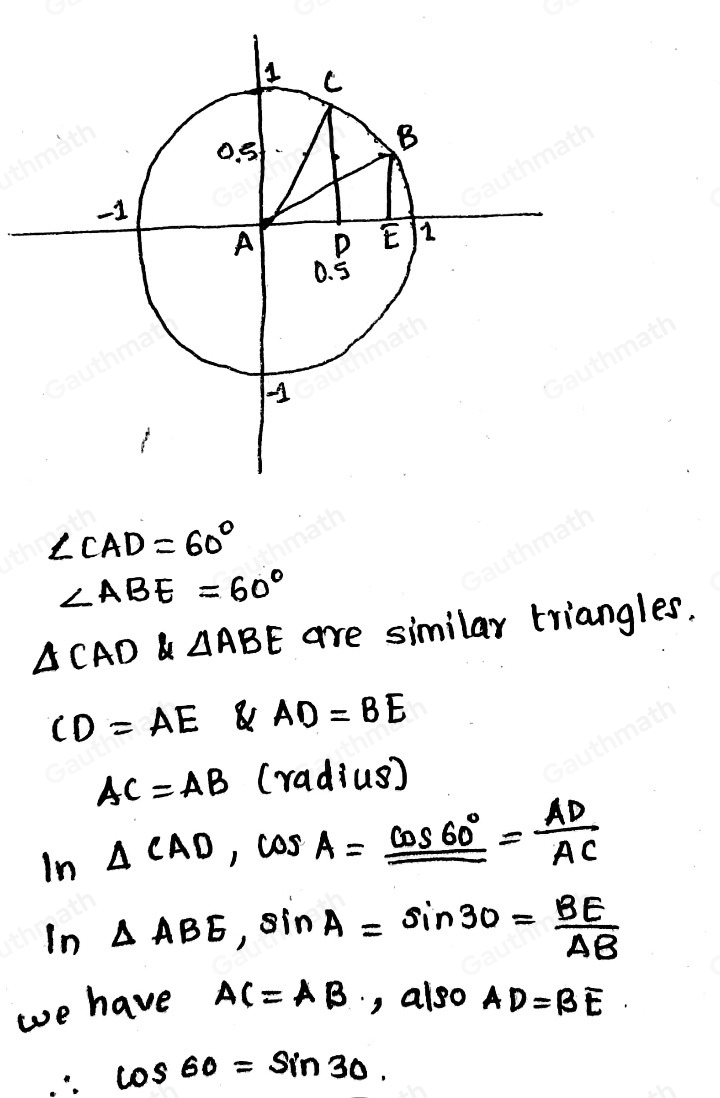
Which of the following explains why cos 60 ° =sin 30 ° using the unit circle? The side opposite a 30 ° angle is the same as the side adjacent to a 60 ° angle in a right triangle. On a unit circle, the y sin distance of a 30 ° angle is the same as the xcos distance of a 60 ° angle. The side opposite a 30 ° angle is the same as the side adjacent to a 60 ° angle in a right triangle. On a unit circle, the xsin distance of a 30 ° angle is the same as the y cos distance of a 60 ° angle. The ratios describe different sides of the same right triangle. On a unit circle, the ysin distance of a 30 ° angle is the same as the xcos distance of a 60 ° angle. The ratios describe different sides of the same right triangle. On a unit circle, the x sin distance of a 30 ° angle is the same as the y cos distance of a 60 ° angle.
Question