Fx=-x5+9x4-18x3
Question
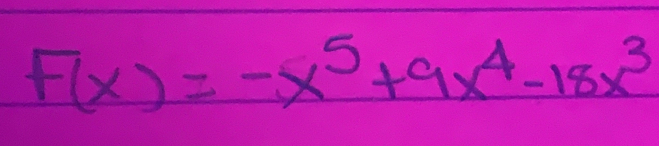
Answer:
(1) Write properties of function: x intercept/zero: x_{1} = 0; x_{2} = 3; x_{3} = 6y intercept: y = 0domain: (-\infty, \infty)type of function: polynomial functionstandard form: F{(x )} = - x^{5} + 9 x^{4} - 18 x^{3}factorized form: F{(x )} = - x^{3} (x - 6) (x - 3)even/odd/neither: neitherbounce/cross x axis: x = 0, cross, x = 3, cross, x = 6, crossincreasing interval: x = 0 , [\dfrac{18}{5} - \dfrac{3 \sqrt{6}}{5}, \dfrac{18}{5} + \dfrac{3 \sqrt{6}}{5}]decreasing interval: (-\infty, \dfrac{18}{5} - \dfrac{3 \sqrt{6}}{5}] , [\dfrac{18}{5} + \dfrac{3 \sqrt{6}}{5}, \infty)number of possible real zeros: 3number of possible turning points: 4order/degree: 5leading term: - x^{5}leading coefficient: -1constant term: 0end behavior: as x →\infty,F(x)→ -\infty; as x →-\infty,F(x)→ \inftygraph: https://p16-ehi-va.gauthmath.com/tos-maliva-i-ejcjvp0zxf-us/7422f4fc09a943af910132e7fd19f1d7~tplv-ejcjvp0zxf-scale:800:800.png
solved
algebra
11 months ago
9634